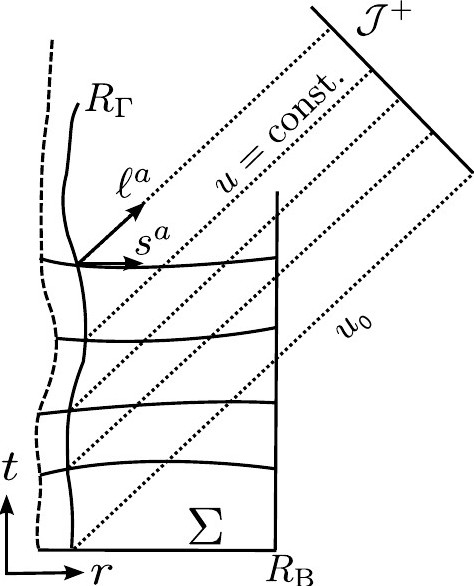
I and collaborators have developed and applied the gravitational-wave extraction technique of Cauchy-characteristic extraction (CCE) to simulations of binary black hole mergers, stellar collapse, and binary neutron star mergers to compute the first unambiguous and gauge-invariant GW signal ever extracted for these problems, allowing me to measure, for the first time, the non-linear memory effect in binary black hole mergers. Without gauge-invariant and mathematically unambiguous gravitational-wave extraction, the computed gravitational-wave forms extracted from a numerical spacetime contain large systematic errors on the order of 10%. However, gravitational-wave detectors data analysis requires an error margin that is significantly smaller. In cauchy-characteristic extraction, the strong field region around, e.g. two orbiting black holes is modeled via standard Cauchy initial boundary value problems. Within a finite radius from the source, on a worldtube, metric data is collected during the evolution. This metric data serves as inner boundary data for a subsequent characteristic evolution. Characteristic evolutions are very efficient at modeling the gravitational-wave far-field region, and allow one to place future null infinity on the computational grid via compactification of the radial coordinate direction. Future null infinity is the region of spacetime that any light ray hits after an infinite amount of time. It is only in this region where gravitational waves can be unambiguously disentangled from the curvature of the backround spacetime.
The corresponding publications (here, here, and here) mark a breakthrough in numerical relativity computations.